27.46 Wheatstone bridge
Chapter 27 Problem 46
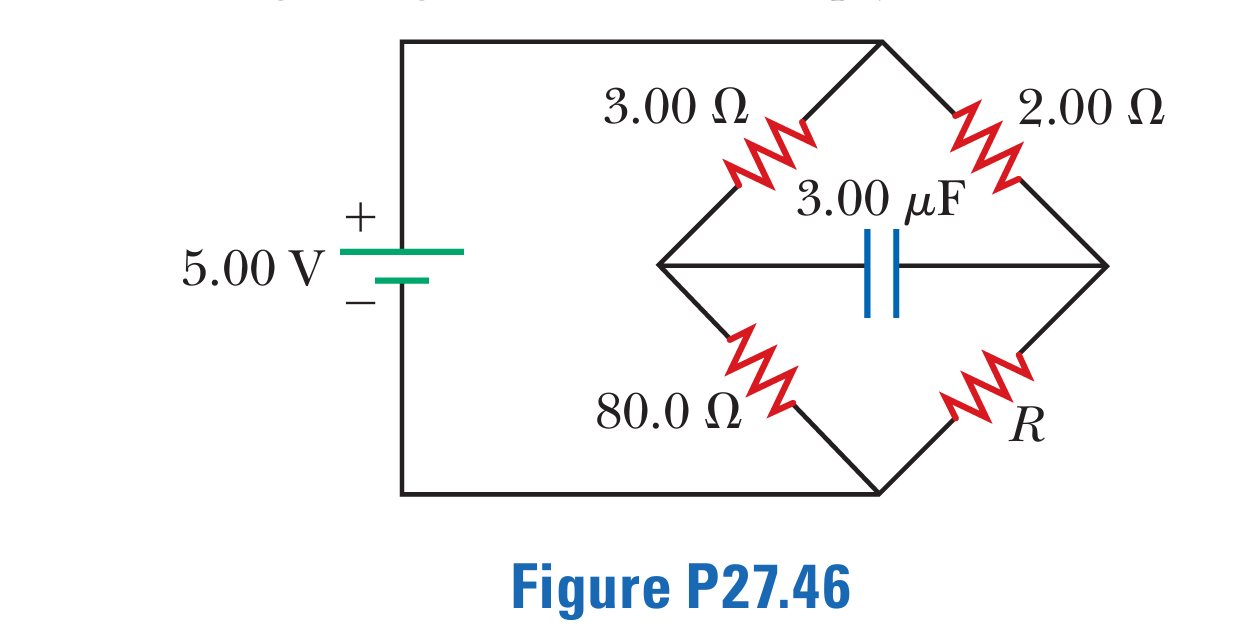
(a) Determine the equilibrium charge on the capacitor in the circuit of Figure P27.46 as a function of R. (b) Evaluate the charge when R 5 10.0 V. (c) Can the charge on the capacitor be zero? If so, for what value of R? (d) What is the maximum possible magnitude of the charge on the capacitor? For what value of R is it achieved? (e) Is it experimentally meaningful to take R 5 `? Explain your answer. If so, what charge magnitude does it imply?
Solution
One way of solving this problem is via Kirchhoff rules. Let \( i1 \) be the current from the positive terminal, \(i2\) the current through the \( 3 \Omega \) resistor, \(i3\) the current through the \( 2 \Omega \) resistor, \(i4\) the current trough the \( 80 \Omega \) resistor , \(i5\) the current trough the \( R \) resistor, and finally \(i\) the current trough the capacitor.
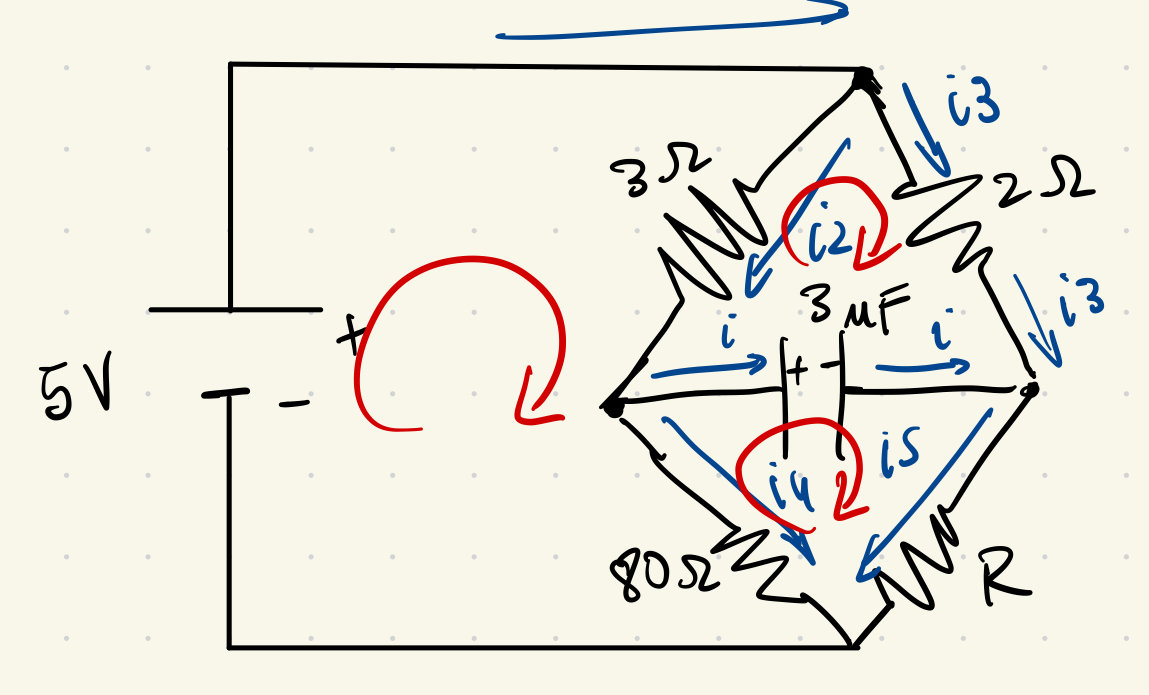
With this distribution of currents and loops the equations are as follows:
\begin{equation} i1 - i2 - i3 = 0 \end{equation} \begin{equation} i2 - i - i4 =0 \end{equation} \begin{equation} i3 + i -i5 = 0 \end{equation}
\begin{equation} 5V - 3\Omega \, i_2 - 80\Omega \, i_4 = 0 \tag{4} \end{equation}
\begin{equation} 3\Omega \, i_2 - 2\Omega \, i_3 + \frac{q}{3\mu F} = 0 \tag{5} \end{equation}
\begin{equation} 80\Omega \, i_4 - R i_5 - \frac{q}{3\mu F} = 0 \tag{6} \end{equation}
These are the mesh equations for the circuit.
The maximum charge occurs when the current through the capacitor is zero:
\begin{equation} i = 0 \quad \Rightarrow \quad \text{from equations (2) and (3):} \end{equation}
\begin{equation} i_2 = i_4 \quad \text{and} \quad i_3 = i_5 \end{equation}
Now we just need to isolate the charge \( q = Q_{\text{max}} \). From equation (6):
\begin{equation} Q = 3\mu F \left( 80\Omega \, i_4 - R i_5 \right) \end{equation}
Or equivalently:
\begin{equation} Q = 3\mu F \left( 80\Omega \, i_2 - R i_3 \right) \end{equation}
From equation (5):
\begin{equation} i_3 = \frac{3}{2} i_2 + \frac{Q}{2R \cdot 3\mu F} \end{equation}
Substitute into the expression for ( Q ):
\begin{equation} Q = 3\mu F \cdot 80\Omega \, i_2 - 3\mu F \cdot R \left( \frac{3}{2} i_2 + \frac{Q}{2R \cdot 3\mu F} \right) \end{equation}
\begin{equation} = i_2 \left( 3\mu F \cdot 80\Omega - 3\mu F \cdot \frac{3R}{2} \right) - \frac{RQ}{2\Omega} \end{equation}
Factor out and rearrange:
\begin{equation} Q \left( 1 + \frac{R}{2\Omega} \right) = i_2 \cdot 3\mu F \left( 80\Omega - \frac{3R}{2} \right) \end{equation}
Simplify the right-hand side:
\begin{equation} Q = i_2 \cdot 3\mu F \left( \frac{160\Omega - 3R}{2} \right) \cdot \left( \frac{2}{2\Omega + R} \right) \end{equation}
Which gives:
\begin{equation} Q = i_2 \cdot 3\mu F \left( \frac{160\Omega - 3R}{2\Omega + R} \right) \end{equation}
Finally, from equation (4):
\begin{equation} 5V - 83\Omega \cdot i_2 = 0 \quad \Rightarrow \quad i_2 = \frac{5V}{83\Omega} \end{equation}
Substitute into the previous equation:
\begin{equation} Q_{\text{max}} = \frac{5V \cdot 3\mu F}{83\Omega} \left( \frac{160\Omega - 3R}{2\Omega + R} \right) \end{equation}
Final Expression
\[ \boxed{ Q_{\text{max}} = \frac{15}{83} \left( \frac{160 - 3R}{2 + R} \right) \, \mu C } \]